背景介绍
现实中由于设备限制和实际防护方式,AES的第一轮和最后一轮往往无法被攻击,所以研究中间轮加密是很有必要的。而随着AES轮数的深入,计算复杂度也会对应提升,即假设中要猜测的比特数会增加,因为AES扩散,每个中间字节依赖的密钥字节会越来越多。
2021年,来自荷兰代尔夫特理工大学、拉德堡德奈梅亨大学的Swaminathan等人在Eprint上发表了一篇对AES内轮进行研究的论文,论文在选择明文和自适应选择密文的基础上,对AES的第二轮、第三轮、第四轮以加密模式进行了攻击,对AES的第七轮以解密模式进行了攻击,并将内轮攻击进行了一般化的公式总结。[1]
攻击方法
以第2轮为例,作者通过加密计算过程总结了攻击复杂度等问题。本文公式符号表示如下:pi表示第i个明文字节,ci表示第i个密文字节,vin表示第n轮的S盒的输出结果的第i个字节,uin表示第n轮列混合结果的第i字节,win表示第n轮轮密钥加结果的第i个字节,kin表示第n轮轮密钥的第i个字节,Sn(u)表示第n轮S盒输出结果,γ, θ分别是8bit的常量。其中n取0~10,i取0~15。
首先猜测第二轮S盒后的第一个字节,可以表示为式(1),其中u10为第一个字节第一轮列混合的输出结果,可以表示为式(2),将两式结合之后,得到式(3)。
v02=S2(w01),w01=u01⊕k01(1)
u01=02*v01⊕03*v51⊕01*v101⊕01*v151(2)
v02=S2(02*v01⊕03*v51⊕01*v101⊕01*v151⊕k01)(3)
因为我们关注的是第一个字节密钥,因此在式(2)中v51,v101,v151我们都不需要关注其具体值为多少,所以可以使用一个常量γ代替与他们相关的值,如式(4)所示。继续将该式带入式(3)中,并将式(3)中的v01用k00表示,可以得到最终的式(5)。
γ=03*v51⊕01*v101⊕01*v151(4)
v02=S2(02*S1(p0⊕k00)⊕γ)(5)
在式(5)中,只有k00和γ是我们在攻击时需要猜测的,即需要猜测16bit数据,同时γ的值是受到3个字节的明文影响的,要想使其不变,需要固定3个字节密钥,因此在攻击第二轮的时候,可以同时攻击4个字节密钥,固定12个字节明文。上述公式表示的流程可以由图1表示。
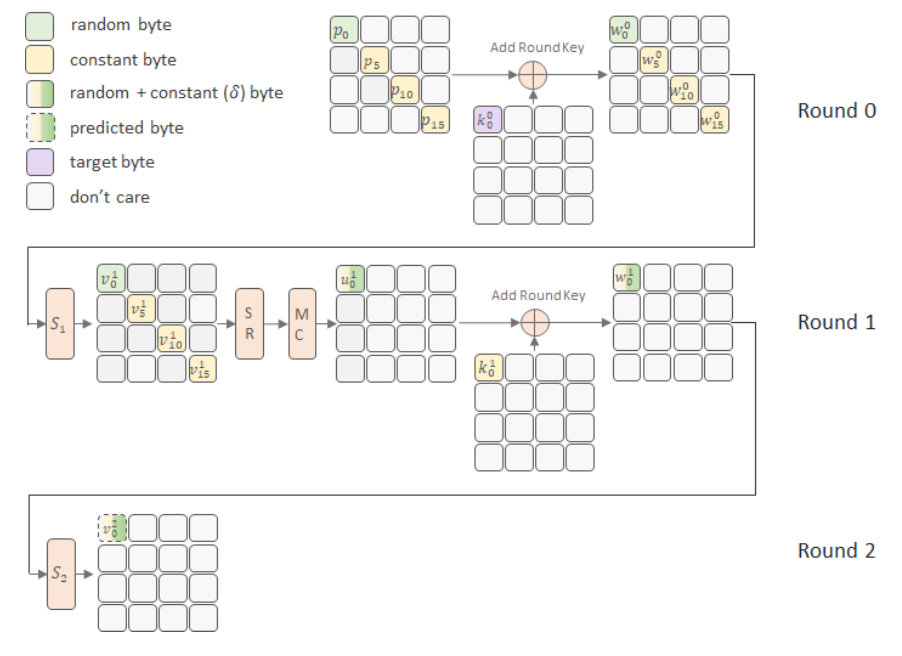
图1 通过AES加密第二轮S盒的输出攻击第一个字节密钥
后续推论与攻击第二轮类似,此处给出第三轮和第四轮S盒输出的表示方式,分别为式(6)、式(7)。
v03=S3(02*S2(02*S1(p0⊕k00)⊕δ)⊕γ)(6)
v04=S4(02*S3(02*S2(02*S1(p0⊕k00)⊕δ)⊕γ)θ)(7)
根据上边的分析,我们可以将攻击一般化,将第j轮S盒之后第i字节表示为式(8)。其中θj需要3*4j-1字节明文固定,同时猜测8*i位来恢复密钥,如图2所示。
vij=Sj(m1*Sj-1(m2*...*S2
(mj-1*S1(pn⊕kn0)⊕θ1)⊕θ2)...⊕θj-1)(8)
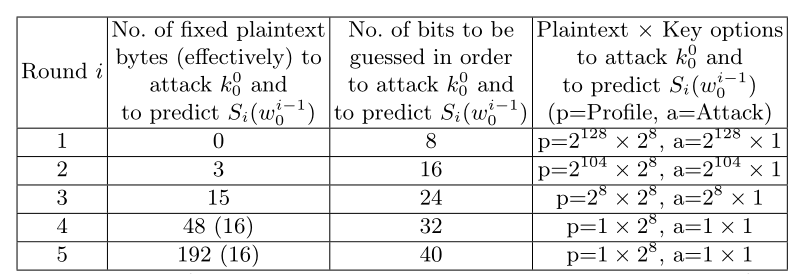
图2 攻击不同轮的分析结果
在图2中,四列数值分别为轮数i,需要固定的明文字节数,需要猜测的比特数以及深度学习方法攻击时训练和攻击可用的波形数。可以看到,随着攻击轮数的深入,需要固定的明文字节数也在增加,因此可以采集的波形数量也会受到限制,到了第四轮,相关能量分析(CPA)只能通过一条波形进行攻击,深度学习侧信道攻击(DL-SCA)建模阶段可以通过更改密钥获得256条波形,但是攻击阶段只能使用固定明文固定密钥的一条波形,因此无论哪一种方式,都难以破解AES密钥。
实验结果
实验使用的波形是作者在基于32位stm32F4的Pinata上采集获得,采集的数据集中波形是不带防护的,并且加密不能在一个时钟内实现多轮AES,作者对比了对正常波形和人为添加了高斯噪声的波形攻击的结果。
以第二轮攻击结果为例,攻击第二轮S盒输出的结果如图3(不带高斯噪声)和图4(添加高斯噪声)所示,其中纵坐标为正确密钥和值的排名,排名空间为216,即65536。在图3中,DL-SCA使用7500条波形训练,500条波形验证,攻击时238条波形成功恢复正确密钥和的值,普通CPA用2000条进行攻击,重复100次实验,正确密钥排名为第6。添加高斯噪声后,DL-SCA使用139条波形后成功恢复正确密钥和的值,普通CPA恢复正确密钥的排名为352,即无法得到正确密钥值。
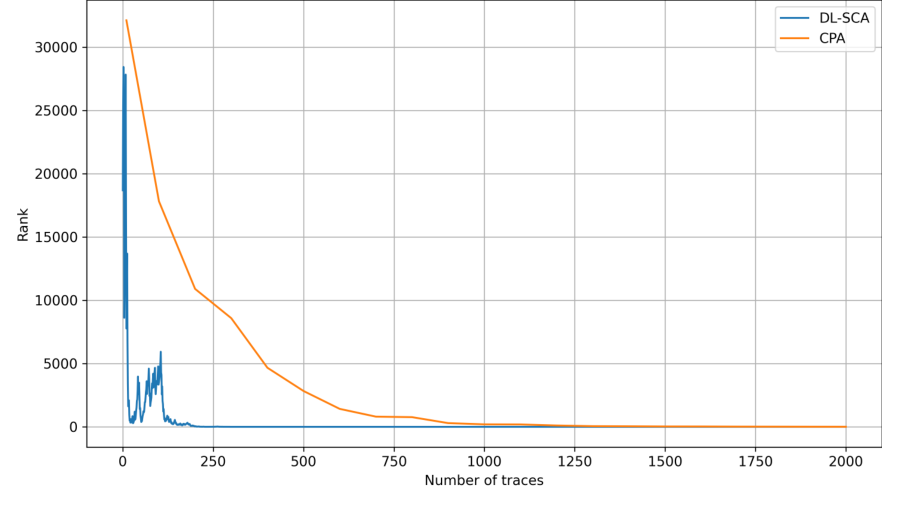
图3 攻击AES第二轮S盒输出的结果
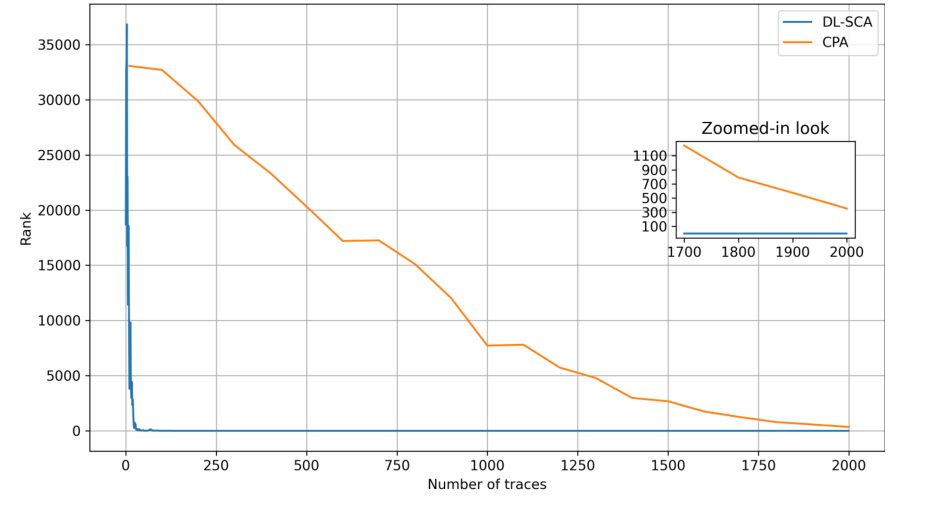
图4 攻击AES第二轮S盒输出的结果(添加高斯噪声)
攻击第三轮S盒输出的结果如图5(不带高斯噪声)和图6(添加高斯噪声)所示,其中纵坐标为正确密钥以及γ值和δ值的排名,排名空间为224。因为此时波形数量受到限制,所以DL-SCA实验使用了2000条波形训练,500条波形验证,500条波形攻击。在不带高斯噪声的情况下,只使用11条波形便恢复了正确密钥,而普通CPA正确密钥的排名分别在75条波和110条波时成为第一。再添加了高斯噪声之后,虽然DL-SCA在使用34波形之后找到了正确密钥,但是CPA使用了500条波形也无法找到正确密钥。
作者对第四轮进行了同样的实验,但是由于波形数量限制,即使在之前实验表现优异的DL-SCA也无法通过第四轮破解AES的密钥。
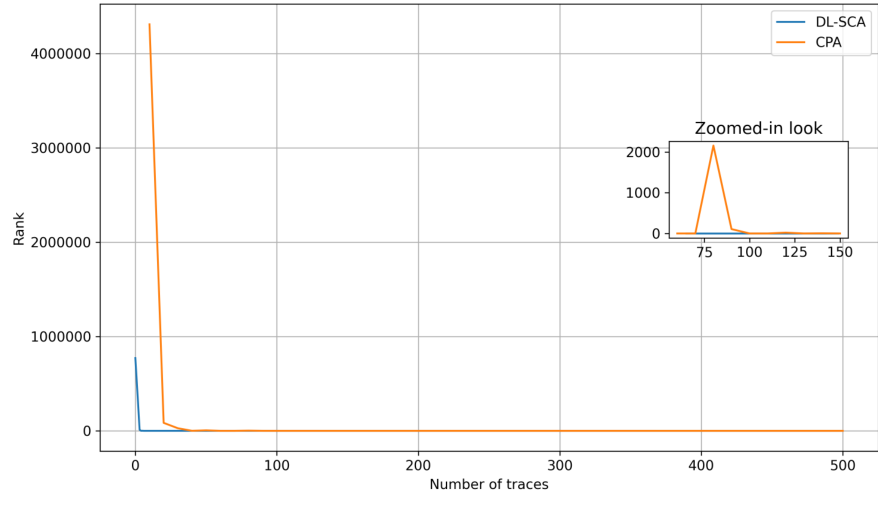
图5 攻击AES第三轮S盒输出的结果
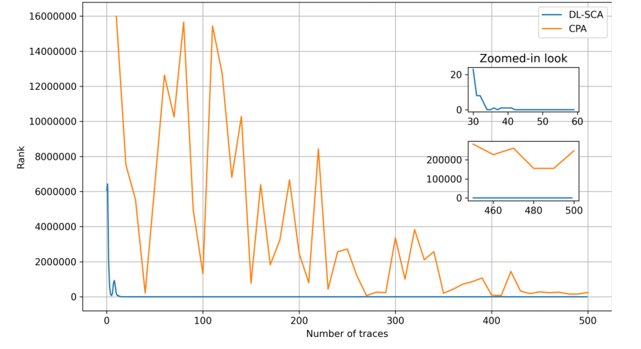
图6 攻击AES第三轮S盒输出的结果(添加高斯噪声)
总结
本文提出了在AES加密下攻击内轮中间字节的通用公式,并证明对第二轮和第三轮的攻击是可行的,对第七轮之后攻击也是可行的。同时,文章对比了DL-SCA和CPA的结果,实践结果证明,DL-CPA相比于CPA,在各种情况下更容易恢复正确密钥,而CPA受到数据复杂度等因素高度限制,难以通过AES内轮恢复AES正确密钥。最后,我们相信在对于深度学习进一步研究之后,可以实现在内轮4~6轮之间进行攻击。
参考资料
[1] Sudharshan Swaminathan, Lukasz Chmielewski, Guilherme Perin, Stjepan Picek: Deep Learning-based Side-channel Analysis against AES Inner Rounds. IACR Cryptol. ePrint Arch. 2021: 981 (2021)

很赞哦! (119)
下一篇:什么是IPS?如何对其进行调整